1. W3HexSchool
  2. 客座投稿
  3. [資料結構] 樹 Tree

hannahpun 已發佈 2019-11-16

[資料結構] 樹 Tree

這一篇會介紹資料結構 Tree 跟運用在前端的哪邊 (雖然我相信閱讀這篇的人一定會很少 XD)

若讀者還有興趣讀下去，但完全沒學過演算法或資料結構，可以參考我之前在 IT 鐵人賽寫的一系列文章 前端工程師用 javaScript 學演算法

images

為什麼會寫這篇 ?

資料結構實在太多種．大致上分為 Linear (Array、Linked List 、Stack、Queue..) 跟 Non-Linear (Tree、Graphs...)，自己當初是從零開始學演算法/資料結構，所以先 Skip 掉看起來很難而且也不知道用在前端哪邊的 Non-Linear data structure。沒想到在面試還是被問到!

面試官: 請問 DOM 是哪種資料結構
我: 你是在問 DOM Tree 嗎?
面試官: 答對了，就是 Tree (沒想到這麼容易)
面試官: 那 DOM Tree 搜尋的時間複雜度是什麼?
我: .....

原來我每天都在碰的 DOM，就是 Tree 資料結構啊 ! 那看來一定要來瞭解一下 Tree 這個資料結構了

什麼是 Tree?

images
樹（Tree）是一種無順序的資料結構，方便快速找資料。為什麼會叫 Tree，因為這種資料結構的確像極倒過來的樹．在生活中也常看到 Tree 的應用，例如 web sitemap、淘汰賽比賽圖、族譜等。

在開始介紹之前，先來認識一下相關專有名詞

  1. 樹根結點 (root): 就是最上面的结點 (node)。每個 tree 只會有一個 root
  2. 子樹 (child tree): 由结點 (node) 和其後代構成
  3. 子结點（child node): 有父结點的结點，所以基本上除了 root 都是
  4. 葉结點或稱外部结點（leaf): 沒有子结點的結點
  5. 结點深度（depth): 祖先結點數量。以下圖來說 body depth 就是 0， img depth 是 2
  6. 樹的高度（height): 最大深度到第幾層。以下圖來說 body height 就是 2， img height 是 0

下圖示意用，所以就列代表而已( 例如 child tree 應該有三個)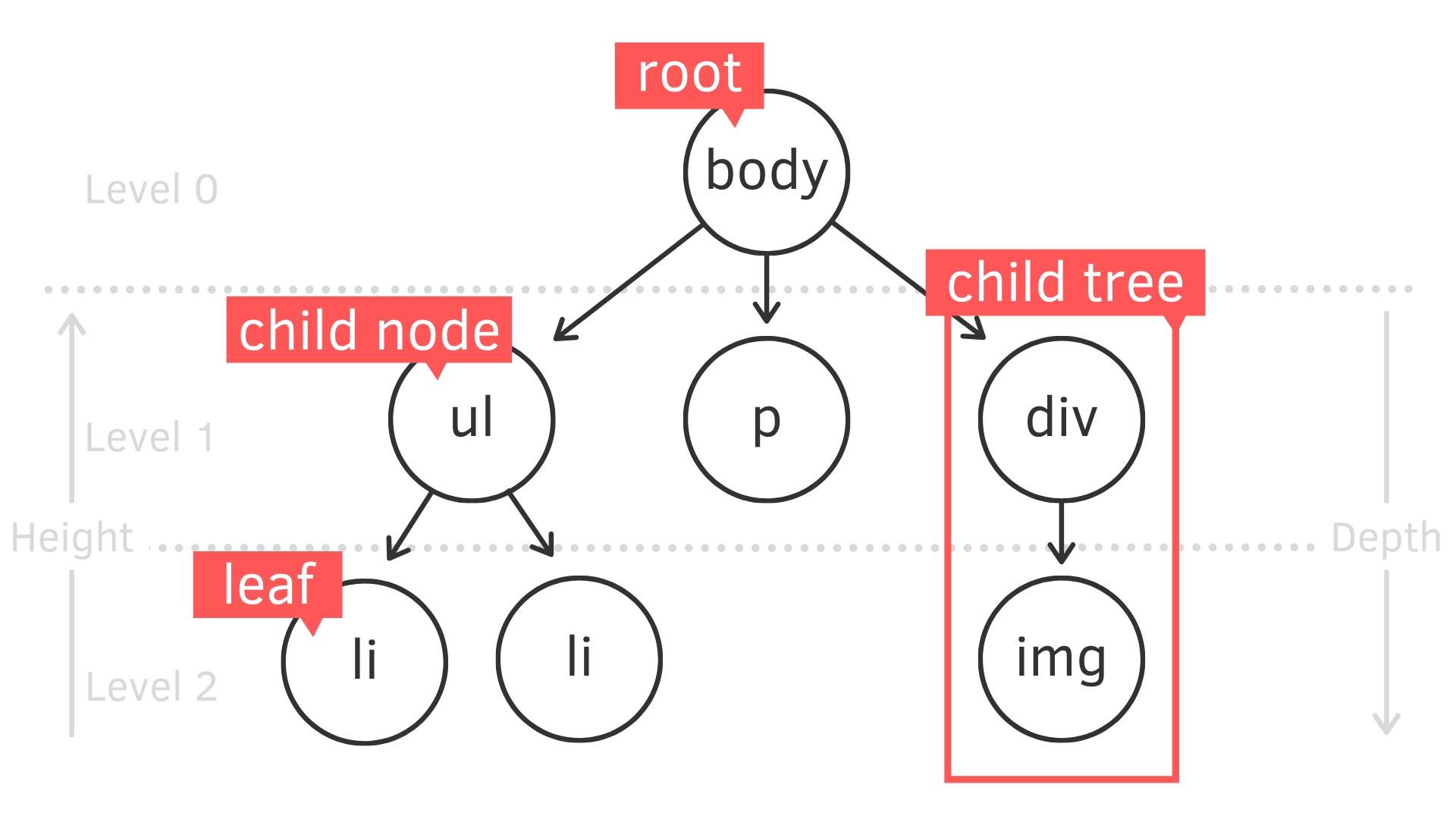
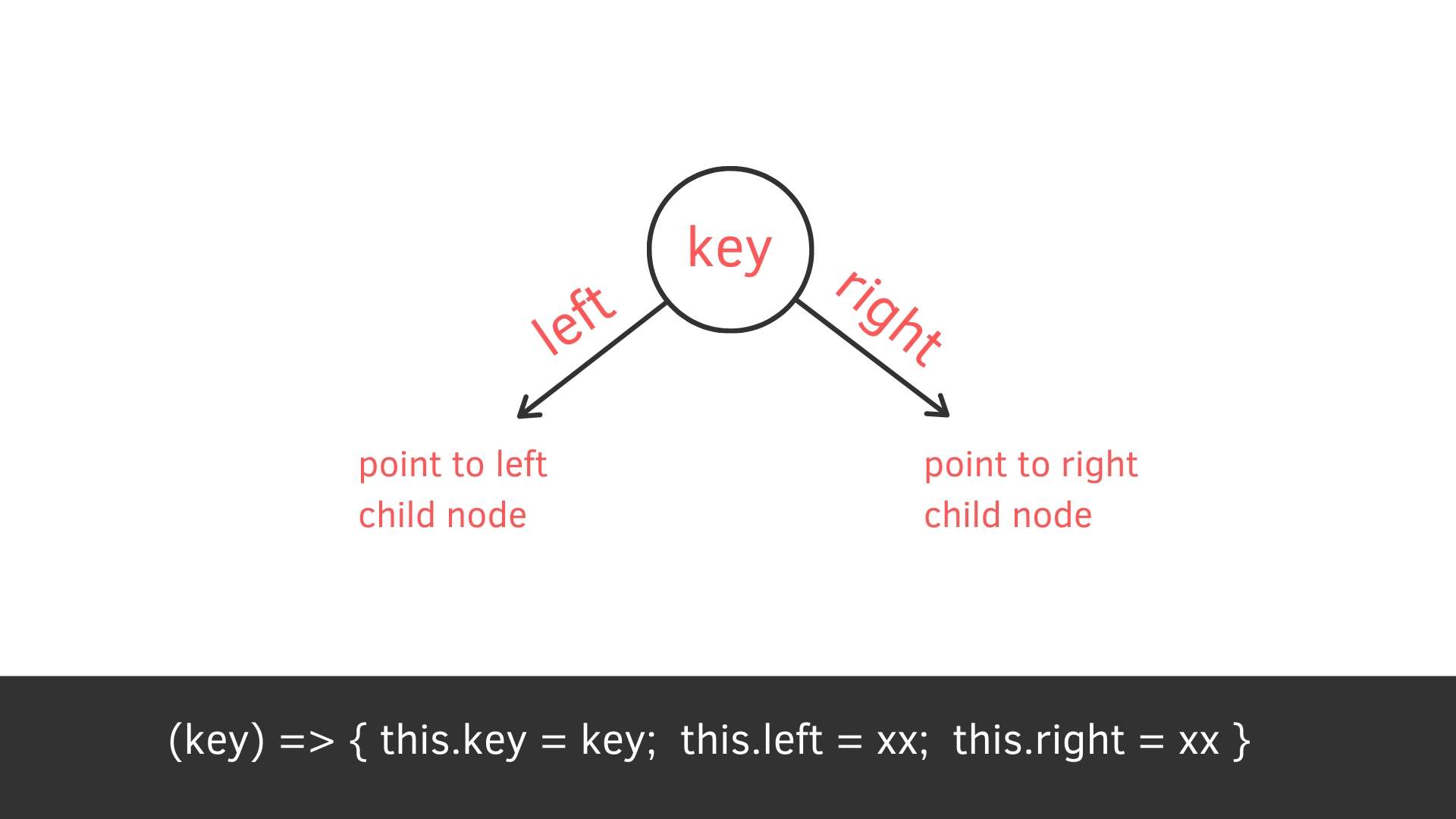
images
若把其中一個 node 拿來看，他會包括

  • key 值
  • 指向的子代

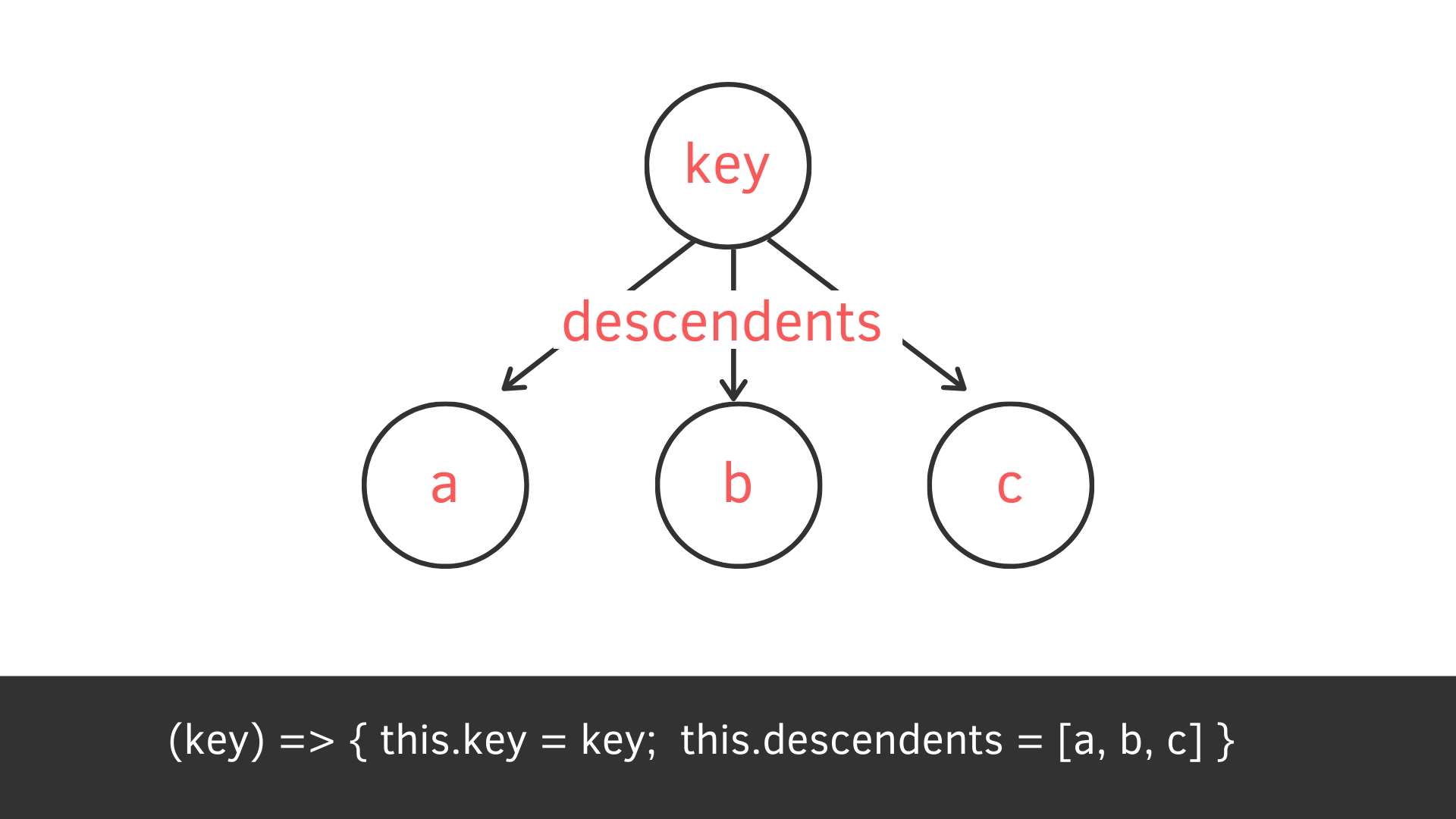
images

class Tree {
    constructor(key){
        this.key = key;
        this.descendents = [];
    }    
}

Binary Search Tree

Tree 其實非常多種類型，例如紅黑樹、二元樹、二元搜尋樹等等。DOM 是一般的樹類型，而這邊也介紹一下最容易入門的二元搜尋樹 (Binary Search Tree)

二元搜尋樹 Binary Search Tree 是二元樹 (Binary Tree) 的一種，他的演算法可以高效的插入、尋找、刪除結點，是很常見的資料結構之一。

規則是每個 node 下面最多兩個 child node

  • 一個是左子結點，放比父結點小的值
  • 一個是右子結點，放比父結點大的值

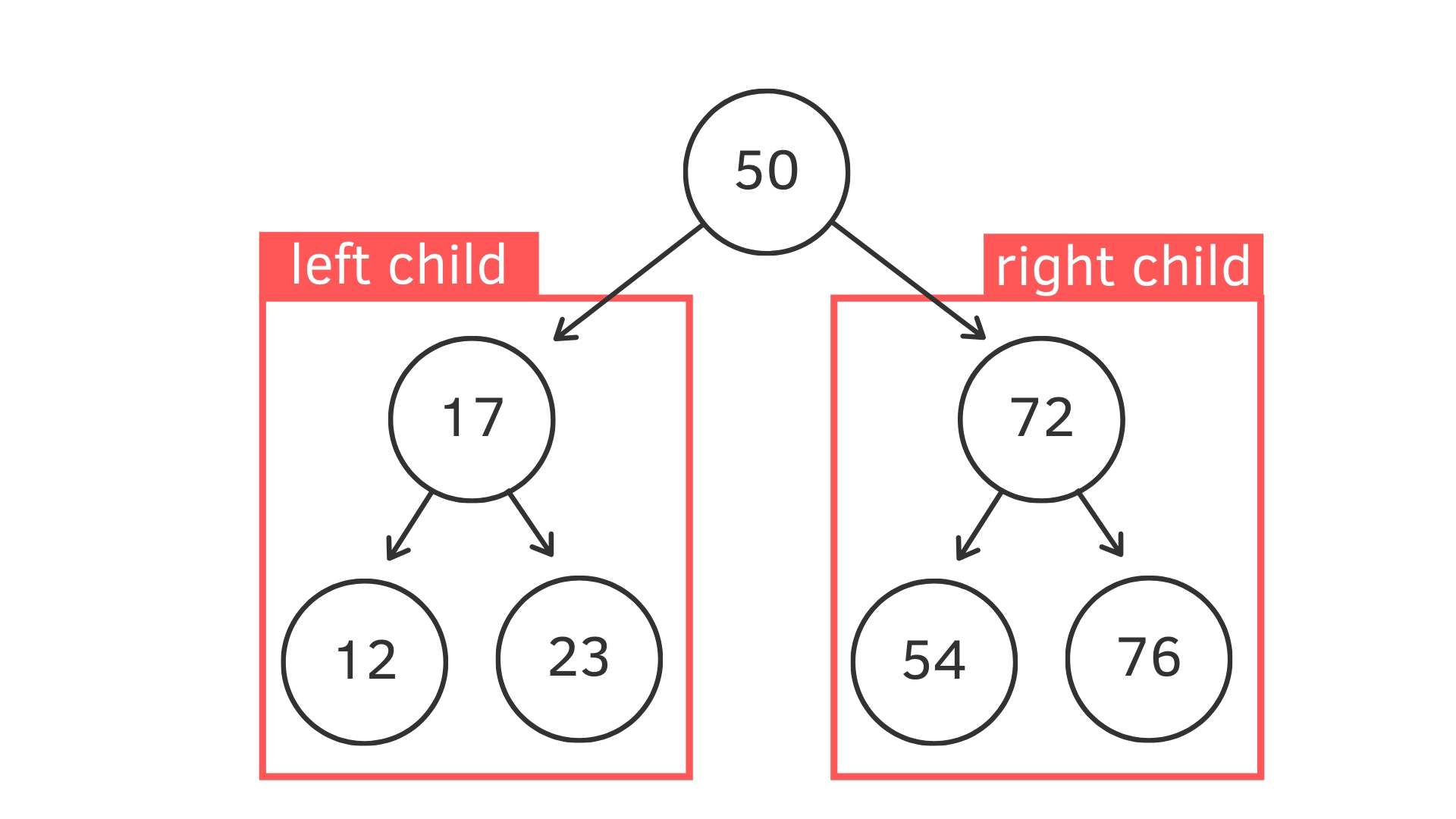
images
通常一個 Binary Search Tree 會有以下這些方法 （這邊不會真正把每個方法的程式碼打出來，只是想要介紹概念）

class BinarySearchTree {
    constructor(key){
        this.key = key;
        this.left = null;
        this.right = null;
    }    
    let root = null;

    // Method
    // 插入 Key 鍵
    insert(key){}

    // 找是否有這個 Key 找到 return true, 沒找到 return false
    search(key){}

    // 透過中序遍歷所有結點
    inOrderTraverse(){}

    // 透過先序遍歷所有結點
    preOrderTraverse = function() {};

    // 透過後序遍歷所有結點
    postOrderTraverse = function() {};

    // 回傳樹中最小值/鍵
    min = function() {};

    // 回傳樹中最大值/鍵
    max = function() {};

    // 從樹中移除某個鍵
    remove = function(key) {};
}

node

Binary Search Tree 的子結點只會最多兩個 (left and right)

/* 建立二元樹 Node 類別，會有
 - 一個存放資料的 key(鍵) 
 - 指向左子結點指標
 - 指向右子結點指標
*/
constructor(key){
    this.key = key;
    this.left = null;
    this.right = null;
}

images

insert (key)

根結點開始比較

  • 若 < parent node 則從 left child 再繼續比
  • 若 > parent node 則從 right child 再繼續比

以新結點 19 來說．總共比了三次

19 < 50 所以往 "左邊" 子結點繼續比較
19 > 17 所以往 "右邊" 繼續比較
19 < 23 最後放在 "右邊"

看圖比較清楚，最後會新增在 23 node 下面的"右邊"子結點

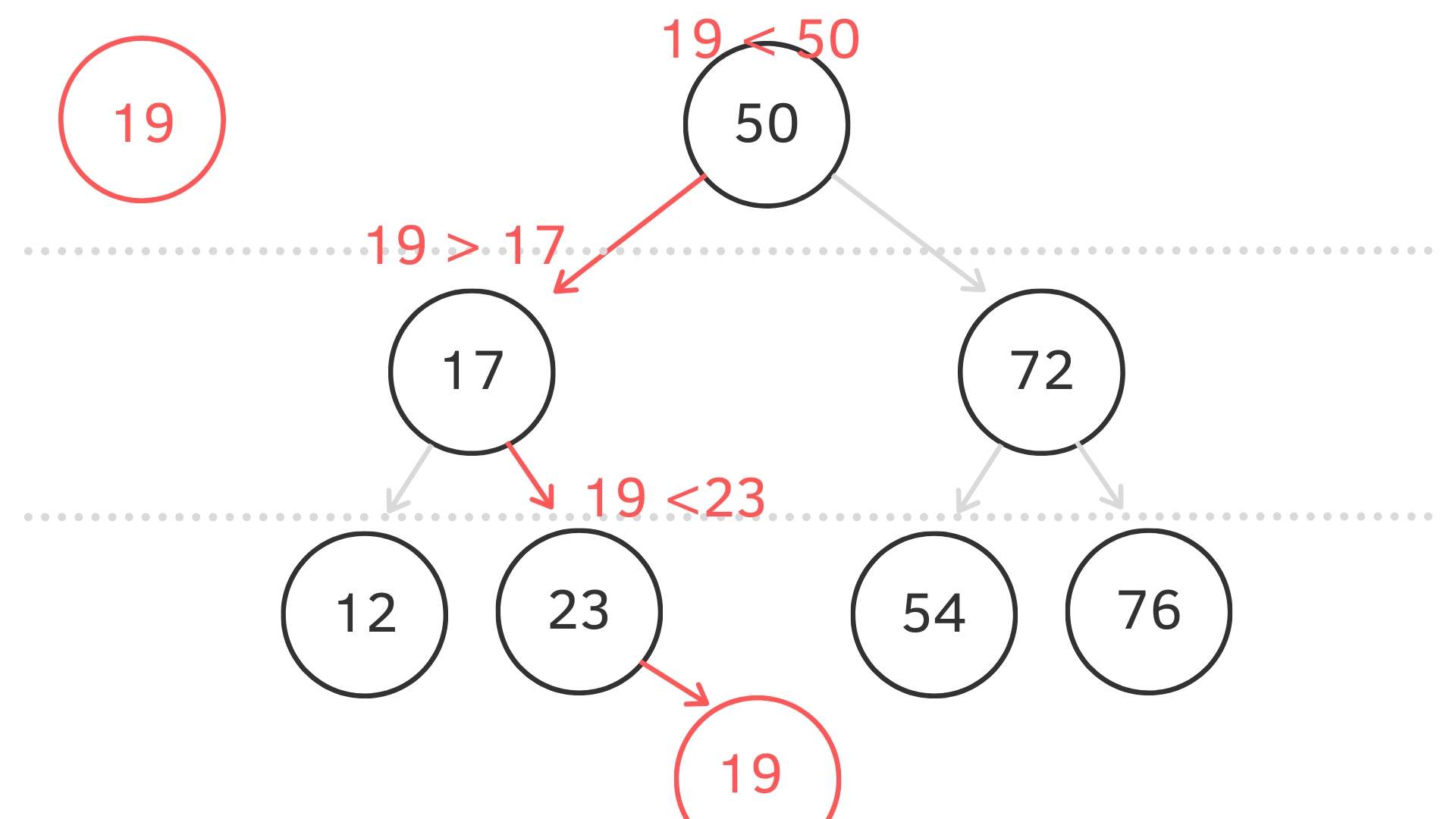
images

Min / Max

Binary Search Tree 最大的值就一定在最右邊，而最小值一定在最左邊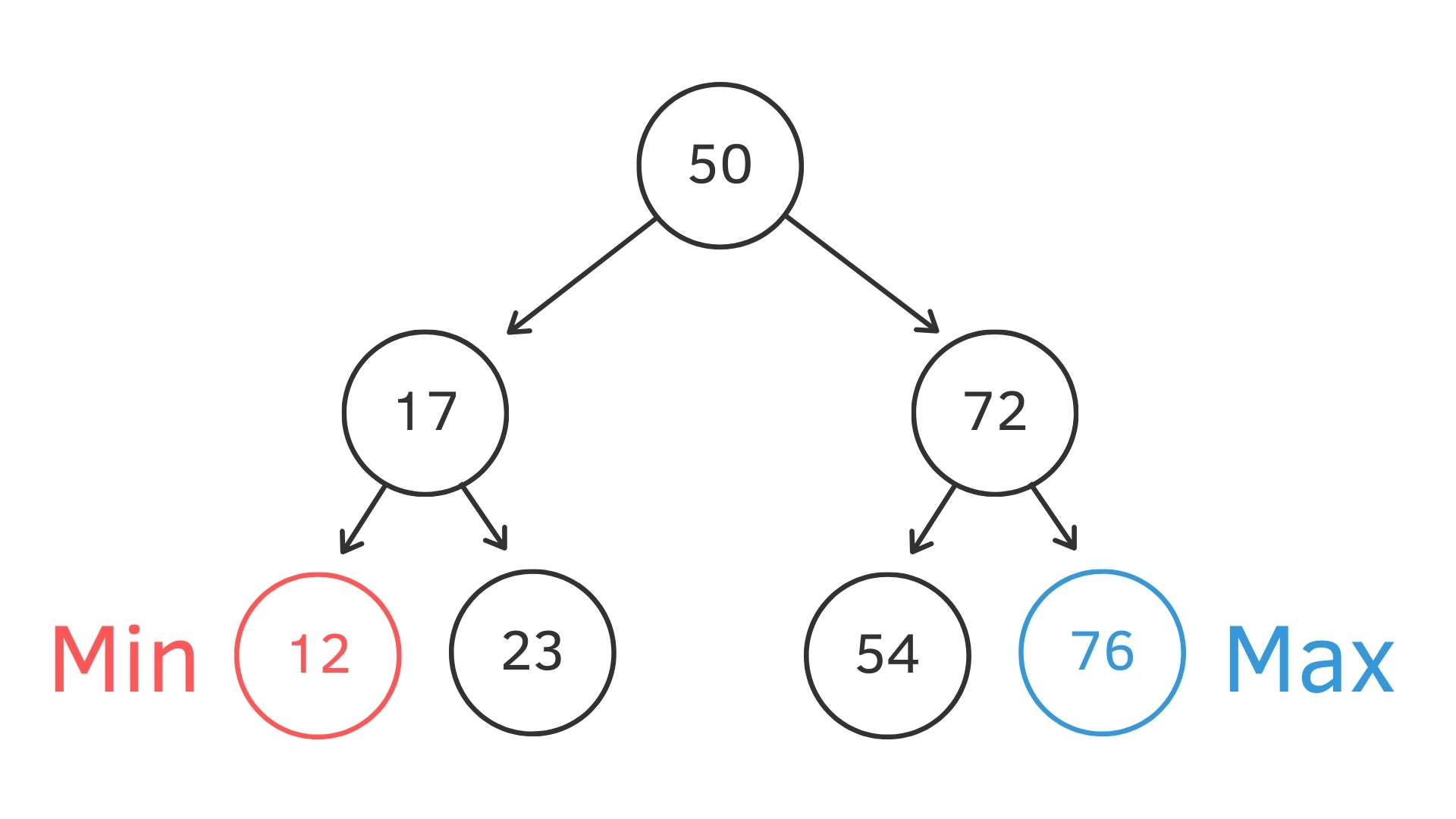
images

BFS vs. DFS

  • BFS: Breadth-First Search 廣度優先搜尋
  • DFS: Depth-first Search 深度優先搜尋

這也是面試常被考概念之一，直接看圖比較好理解怎麼運作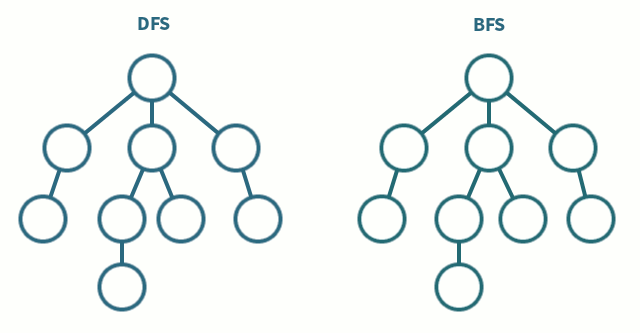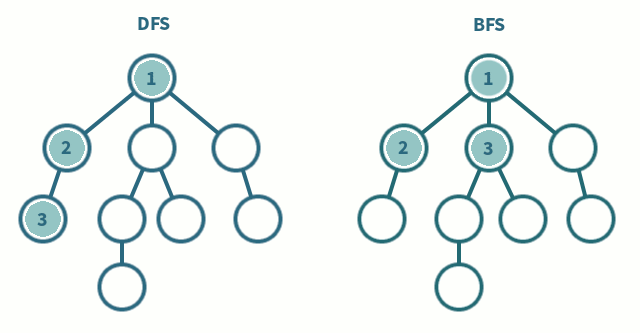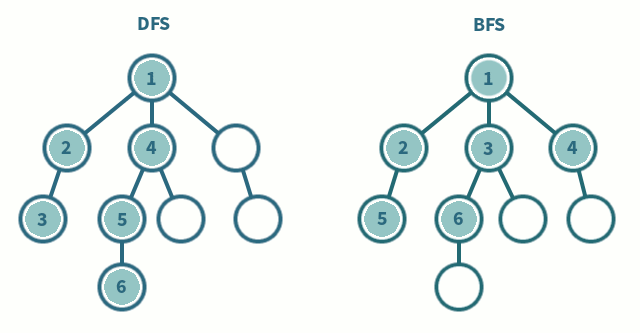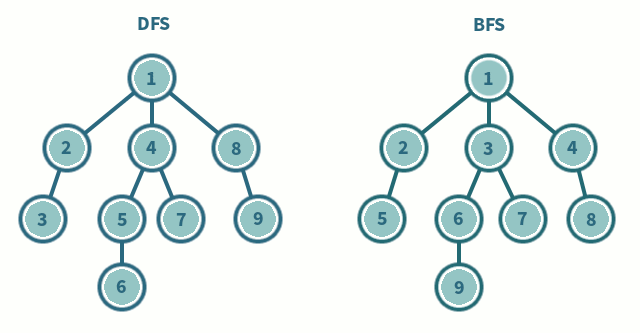
images

<!-- 允許我先客製 HTML tag 比較好解釋 -->
<content>
    <sidebar>
        <menu></menu>
    </sidebar>
</content>
<main>
    <post></post>
    <img />
</main>

若將上面 HTML 架構轉換成 DOM Tree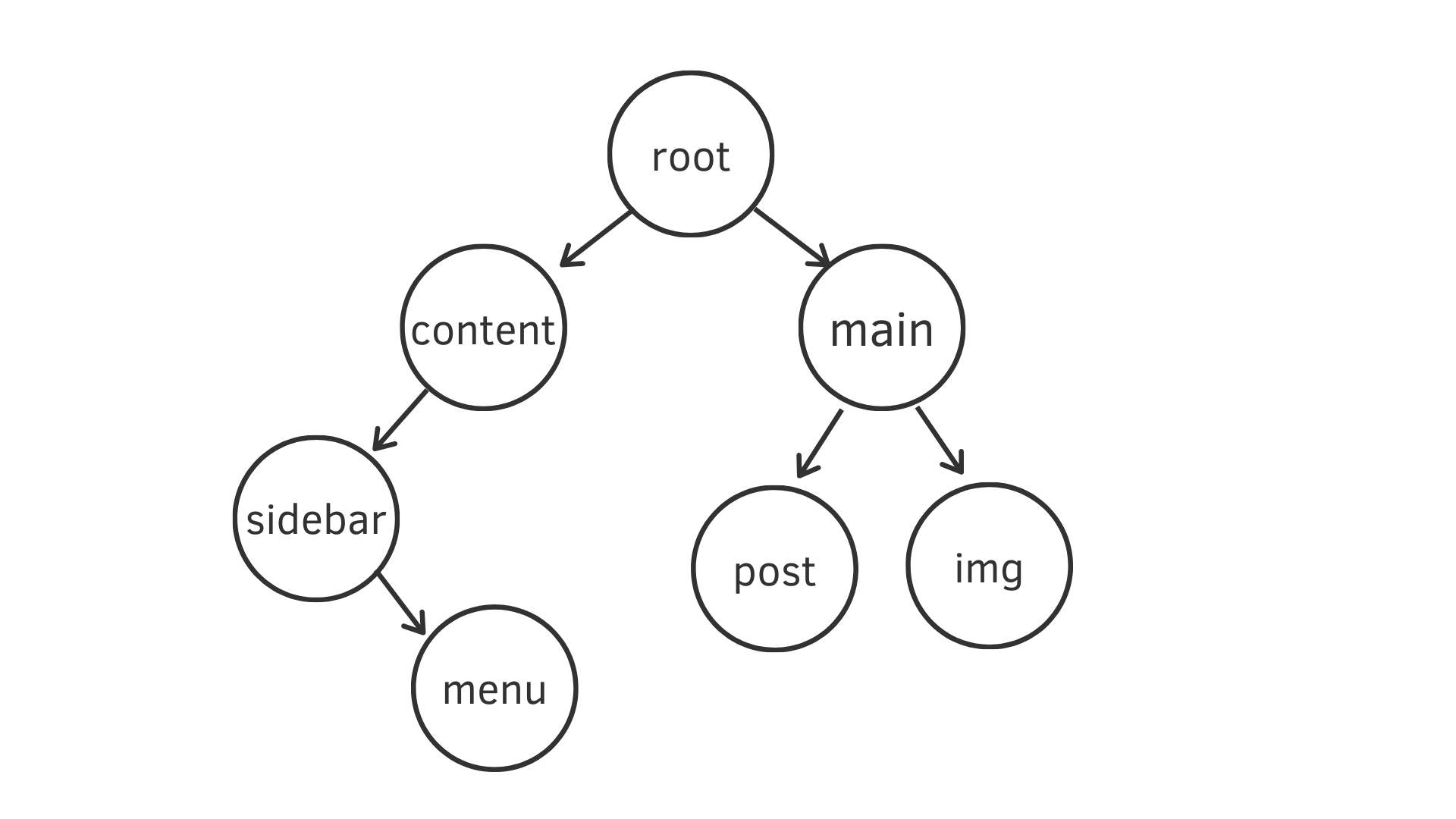
images

使用 DFS，查找順序就會是

root -> content -> sidebar -> menu -> main -> post -> img

而使用 BFS，查找順序就會變成是

root -> content -> main -> sidebar -> post -> img -> menu

結論

恩，看資料結構總是讓人卻步 (要不是面試會考我八輩子也不會看)，畢竟我們也不是寫瀏覽器底層的人，但這些概念一直頻繁實作在不同 Framework 跟 library 裡面，明白他們才能讓自己寫出更高效能的程式。

況且現在轉職到前端的人實在太多，都跟我一樣在學校沒有被教過這些看似無聊卻很重要的理論 ，但相信這些都是成為資深工程師的必學理論之一! (前端沒這麼好混的啊)

另外懂了 Tree 概念再來看 DOM tree 真的容易很多呢

參考資料

關於筆者

暱稱：hannahpun

介紹：熱愛前端，不斷學習的前端工程師

標籤雲 標籤雲

文章列表 文章列表